Monografia apresentada ao Curso de Estatística da Universidade Federal de Minas Gerais como parte dos requisitos para a obtenção do Grau de Estatístico.
Resumo
O mercado de seguros no Brasil tem mostrado um crescimento significativo. No primeiro trimestre de 2024, a arrecadação do setor de seguros ultrapassou R$ 100 bilhões, representando um aumento de 13,7% em relação ao mesmo período de 2023. Os valores que retornaram à sociedade por meio de indenizações, resgates, benefícios e sorteios, somaram um montante de R$56,7 bilhões. Em 2023, o setor de seguros cresceu 9% e superou R$380 bilhões arrecadados.
No contexto da aplicação de Modelos Gráficos Mistos Variantes no Tempo (MGM) aos dados de Prêmios e Sinistros do mercado de seguros brasileiro, destaca-se a capacidade desse modelo em capturar a dinâmica temporal das interações entre variáveis complexas. Os MGMs são uma extensão poderosa dos modelos gráficos tradicionais, permitindo a análise de múltiplos tipos de variáveis (contínuas, categóricas, etc.) e sua evolução ao longo do tempo através de abordagens como modelos mVAR e ponderação de kernel.
A aplicação desses modelos revela-se crucial para entender como eventos externos e mudanças regulatórias impactam a estrutura de prêmios e sinistros ao longo dos anos utilizando a base de dados de Prêmios e Sinistros do sistema de estatísticas da SUSEP. Essas “intervenções” influenciam a frequência e magnitude dos sinistros e a arrecadação de prêmios, tornando o MGM uma ferramenta essencial para seguradoras na gestão de riscos e na formulação de políticas.
Além de analisar as relações entre prêmios e sinistros, os MGMs permitem explorar as centralidades temporais das variáveis, como grau, proximidade e mediação, ao longo do tempo. Essas medidas fornecem insights sobre a importância relativa das variáveis na rede de interações, destacando como a estrutura da rede evolui e se adapta às condições do mercado de seguros.
Em resumo, a utilização de Modelos Gráficos Mistos Variantes no Tempo oferece uma perspectiva detalhada e dinâmica das complexas interações dentro do mercado de seguros, contribuindo significativamente para uma compreensão mais profunda das tendências e padrões ao longo do tempo. Essa abordagem não só enriquece a análise estatística, mas também orienta decisões estratégicas e políticas no setor de seguros, promovendo maior eficiência e adaptação às mudanças do ambiente regulatório e econômico.
Palavras-chave: seguros, prêmios, sinistros, modelos gráficos, centralidades.
Abstract
The insurance market in Brazil has shown significant growth. In the first quarter of 2024, the sector’s revenue exceeded R$ 100 billion, representing a 13.7% increase compared to the same period in 2023. The amounts returned to society through claims, redemptions, benefits, and raffles totaled R$ 56.7 billion. In 2023, the insurance sector grew by 9% and surpassed R$ 380 billion in revenue.
In the context of applying Time-Varying Mixed Graphical Models (TV-MGMs) to the Premiums and Claims data of the Brazilian insurance market, the model’s ability to capture the temporal dynamics of interactions among complex variables stands out. TV-MGMs are a powerful extension of traditional graphical models, allowing for the analysis of multiple types of variables (continuous, categorical, etc.) and their evolution over time through approaches such as mVAR models and kernel weighting.
The application of these models proves crucial for understanding how external events and regulatory changes impact the structure of premiums and claims over the years, utilizing the Premiums and Claims database from SUSEP’s statistical system. These “interventions” influence the frequency and magnitude of claims and the collection of premiums, making TV-MGM an essential tool for insurers in risk management and policy formulation.
Besides analyzing the relationships between premiums and claims, TV-MGMs allow for the exploration of the temporal centralities of variables, such as degree, closeness, and betweenness, over time. These measures provide insights into the relative importance of variables in the interaction network, highlighting how the network’s structure evolves and adapts to market conditions.
In summary, the use of Time-Varying Mixed Graphical Models offers a detailed and dynamic perspective of the complex interactions within the insurance market, significantly contributing to a deeper understanding of trends and patterns over time. This approach not only enriches statistical analysis but also guides strategic decisions and policies in the insurance sector, promoting greater efficiency and adaptation to changes in the regulatory and economic environment.
Keywords: insurance, premiums, claims, graphical models, centralities.
Introdução
O mercado de seguros no Brasil tem mostrado um crescimento significativo. No primeiro trimestre de 2024, a arrecadação do setor de seguros ultrapassou R$ 100 bilhões, representando um aumento de 13,7% em relação ao mesmo período de 2023. Os valores que retornaram à sociedade por meio de indenizações, resgates, benefícios e sorteios, somaram um montante de R$56,7 bilhões. Em 2023, o setor de seguros cresceu 9% e superou R$380 bilhões arrecadados.
Paralalemente, a evolução da ciência de dados e das técnicas estatísticas tem permitido o desenvolvimento de modelos cada vez mais sofisticados para a análise de dados complexos. Um desses avanços é o uso de Modelos Gráficos Mistos Variantes no Tempo (MGM), que oferecem uma abordagem flexível e robusta para modelar a interdependência entre variáveis ao longo do tempo. Vamos quebrar isso para entender melhor sobre o modelo mencionado:
Mistos: Significa que o modelo pode lidar com diferentes tipos de dados ao mesmo tempo. Por exemplo, este modelo pode analisar dados contínuos (como altura ou peso), dados categóricos (como cor dos olhos ou tipo de carro), dados binários (como sim/não ou verdadeiro/falso), entre outros.
Modelo Gráfico: É uma maneira de representar as relações entre variáveis. Imagine um gráfico onde cada ponto é uma variável e as linhas entre os pontos representam as relações entre essas variáveis. Isso nos ajuda a visualizar e entender as complexas interações entre muitas variáveis. Abordaremos mais sobre os modelos gráficos na seção metodológica do método.
Variantes no Tempo: Significa que o modelo leva em consideração como essas relações mudam com o tempo. Isso é útil quando estamos analisando processos que evoluem ao longo do tempo.
Então, em resumo, um Time-Varying Mixed Graphical Model, ou Modelos Gráficos Mistos Variantes no Tempo, no qual chamaremos de MGM ao longo da dissertação, é uma ferramenta que nos ajuda a entender como diferentes tipos de variáveis interagem entre si e como essas interações mudam ao longo do tempo.
Nesta monografia, exploraremos o MGM no contexto dos seguros, especificamente utilizando a base de dados de Prêmios e Sinistros do sistema de estatísticas da SUSEP. A SUSEP, ou Superintendência de Seguros Privados, é uma autarquia federal brasileira que regula o mercado de seguros, previdência privada aberta, capitalização e resseguro. Mas o que são prêmios e sinistros?
Prêmios, são os valores que os segurados pagam às seguradoras para terem direito a uma cobertura de seguro. É como se fosse uma “assinatura” que você paga para a seguradora para que ela possa te ajudar financeiramente caso ocorra algum evento previsto na apólice do seguro.
Sinistros, são os eventos ou ocorrências previstas na apólice de seguro que geram um prejuízo ao segurado. Quando um sinistro ocorre, a seguradora precisa pagar uma indenização ao segurado. Por exemplo, se você tem um seguro de carro e sofre um acidente, o acidente é considerado um sinistro. A seguradora então irá pagar os custos de reparo do carro, conforme previsto na apólice.
Os dados de Prêmios e Sinistros fornecidos pela SUSEP, representam uma rica fonte de informações que podem ser utilizadas para entender as tendências e padrões no mercado de seguros brasileiro. Através da aplicação do modelo gráfico misto MGM a esses dados, esperamos obter insights valiosos que possam informar decisões estratégicas e políticas no setor de seguros.
Esta monografia está organizada da seguinte maneira: fornecemos uma revisão da literatura sobre os modelos gráficos mistos, discutindo sua formulação matemática e suas propriedades. Além disso, descrevemos a base de dados da SUSEP e discutimos como os dados de Prêmios e Sinistros serão preparados para a análise. Ademais, apresentamos os resultados da nossa análise, discutindo as implicações dos nossos achados para a indústria de seguros, através do estudo da evolução temporal dos modelos gráficos mistos variantes no tempo, além de entender as características estruturais dos grafos utilizando centralidades temporais, por exemplo. Finalmente, concluiremos a monografia com uma discussão sobre as limitações do nosso estudo e sugestões para pesquisas futuras.
O objetivo é utilizar um modelo gráfico temporal para entender a estrutura de dependências entre os fatores que influenciam as características do mercado de seguros no Brasil de 2001 a 2023, com foco especial em observar a evolução temporal das características estruturais de centralidade neste modelo gráfico. Vale destacar que há duas versões do MGM, estacionária e auto-regressiva. Nesta monografia optamos pela aplicação da versão estacionária.
Modelos Gráficos
Este tópico foi adaptado a partir do artigo .
Introdução sobre os Modelos Gráficos
Modelos gráficos são famílias de distribuições de probabilidade que respeitam um conjunto de declarações de independência condicional representadas em um grafo não direcionado \(G\). Vejamos a representação de um grafo não direcionado na Figura a seguir.
Um grafo é como uma rede de pontos conectados por linhas. Esses pontos são chamados de “vértices” e as linhas são chamadas de “arestas”. Um grafo não direcionado \(G=(V, E)\) consiste em um vetor de vértices (nós) \(V=\{1,2, \ldots, p\}\) e um vetor de arestas \(E \subset V \times V\). Um subconjunto de vértices \(U\) é um nó de corte sempre que sua remoção quebra o grafo em dois ou mais subconjuntos não vazios, o que equivale a \(U\) sendo o conjunto tal que todos os caminhos dos conjuntos de nós disjuntos \(S\) e \(Q\) passam por \(U\) .
Um clique em um grafo é um grupo vértices onde todos se conectam. Em termos técnicos, é um conjunto de vértices em que cada par de vértices é conectado por uma aresta. Definindo, um clique é um subconjunto \(C \subseteq V\) tal que \((s, t) \in E\), para todo \((s, t) \in C\), onde \(s \ne t\), além disso, é chamado de máximo clique se a inclusão de qualquer outro vértice não o tornaria um clique. O vizinho \(N(s)\) de um vértice \(s \in V\) é o conjunto de nós que estão conectados por uma aresta, \(N(s):=\{t \in V \mid(s, t) \in E\}\). Ao longo da monografia utilizaremos a abreviatura \(X_{\backslash s}\) para \(X_{V \backslash\{s\}}\).
A cada vértice no grafo \(G\) associamos uma variável aleatória \(X_{s}\) tomando valores em um espaço \(\mathcal{X}_s\). Para qualquer subconjunto \(A \subseteq V\), usamos a abreviatura \(X_A:=\left\{X_s, s \in A\right\}\). Para três subconjuntos disjuntos de nós, \(A, B\) e \(U\), escrevemos \(X_A \perp X_B \mid X_U\) para indicar que o vetor aleatório \(X_{A}\) é independente de \(X_{B}\) quando condicionado em \(X_{U}\).
Podemos agora definir modelos gráficos em termos da propriedade de Markov, a qual formaliza a conexão entre distribuição de probabilidade e grafo \(G\) (definição dada por Loh PL e Wainwright MJ, 2012).
Definição 1 (Propriedade Global de Markov). Se \(X_A \perp X_B \mid X_U\) para qualquer \(U\) que é um nó de corte que subdivide o grafo em dois subconjuntso distintos \(A\) e \(B,\) então o vetor aleatório \(X:=(X_{1},\cdot\cdot\cdot,X_{p})\) é Markoviano em relação ao grafo \(G.\)
Observe que o conjunto de vizinhança \(N(s)\) é sempre um nó de corte para \(A=\{s\}\) e \(B=V\setminus\{s \cup N(s)\}\).
No restante desta monografia nos concentraremos nas distribuições da família exponencial, que são distribuições estritamente positivas. Para estas distribuições a propriedade global de Markov é equivalente à propriedade de fatoração de Markov pelo Teorema de Hammersley-Clifford.
Considere para cada clique \(C\) no conjunto de todos os conjuntos de cliques \({{{\cal{C}}}}\) uma função de compatibilidade de cliques \(\psi_{C}(X_{C})\) que mapeia configurações \(x_{C}=\{x_{s},s\in C\}\) para \({\mathrm{R}}^{\dagger}\) tal que \(\psi_{C}\) depende apenas das variáveis \(X_{C}\) correspondendo ao clique \(C\).
Definição 2 (Propriedade de fatoração de Markov). A distribuição de \(X\) fatora de acordo com \(G\) caso possa ser representado como um produto de funções clique
\[\begin{equation} P(X)\propto\prod_{C\in C}\psi_{C}(X_{C}). \label{eq:eq1} \end{equation}\]Esta equivalência implica que se tivermos distribuições que são representadas como um produto de funções clique, então podemos representar as declarações de dependência condicional nesta distribuição num grafo \(G\). Este é o caso das distribuições da família exponencial que usamos nesta monografia
\[\begin{equation} P(X)=\exp\left\{\sum_{C\in C}\theta_{C}\phi_{C}(X_{C})-\Phi(\theta)\right\}, \label{eq:eq2} \end{equation}\]onde as funções \(\phi_{C}(X_{C}) = log\psi_{C}(X_{C})\) são estatísticas suficientes especificadas pelo membro da família exponencial em questão (por exemplo, Gaussiana, Exponencial, Poisson, etc.) \(\theta_{C}\) são parâmetros associados às funções clique e \(\Phi(\theta)\) é a constante de normalização logarítmica
\[ \Phi(\theta)=\log\int_{\mathcal{X}_{C\in C}}\theta_{C}\phi_{C}(X_{C})\nu(d x), \]
O grafo \(G\) representa uma família de distribuições porque suas arestas não indicam a força da dependência e os nós podem representar diferentes distribuições condicionais. Portanto, não há apenas um mapeamento de um a um da função de densidade para o grafo, mas um mapeamento de um para muitos do grafo para as funções de densidade.
Modelos Gráficos Mistos
Nesta seção, introduzimos a classe de modelos gráficos mistos, os quais permitem combinar um conjunto arbitrário de membros univariados condicionais da família exponencial em uma distribuição conjunta.
Considere um vetor aleatório p-dimensional \(X = (X_{1},...,X_{p})\) com cada variável \(X_{s}\) tomando valores em um conjunto potencialmente diferente \(\mathcal{X}_{s}\), e seja \(G = (V,E)\) um grafo não direcionado com \(p\) vértices correspondentes às \(p\) variáveis. Agora suponha que a distribuição condicional do nó \(X_{s}\) condicionada a todas as outras variáveis \(X_{\backslash s}\) seja dada por uma distribuição familiar exponencial univariada arbitrária
\[\begin{equation} P(X_{s}|X_{\backslash s})=\exp\{E_{s}(X_{\backslash s})\phi_{s}(X_{s})+C_{s}(X_{s})-\Phi(X_{\backslash s})\}, \label{eq:eq3} \end{equation}\]onde as funções da estatística suficiente \(\phi_{s}\) e a medida base \(C_{s}(.)\) são especificados pela escolha da família exponencial e o parâmetro canônico \(E(X_{\backslash s})\) é uma função de todas as variáveis, exceto \(X_{s}\).
Essas distribuições condicionais de vértices são consistentes com uma distribuição conjunta sobre o vetor aleatório \(X\), ou seja, é a propriedade de Markov aplicada em relação ao grafo \(G = (V,E)\) com o conjunto de cliques \({\boldsymbol{C}}_{k}\) de tamanho mínimo \(k\) se e somente se os parâmetros canônicos \(\left\{E_{s}(\cdot)\right\}_{s\in V}\) são uma combinação linear de produtos de funções estatísticas suficientes univariadas \(\left\{\phi(X_{r})\right\}_{r\in N(s)}\) de ordem até \(k\)
\[\begin{equation} \theta_{s}+\sum_{r\in{\cal N}(s)}\theta_{s,r}\phi_{r}(X_{r})+\cdot\cdot\cdot+\sum_{r_{1},\ldots,r_{k-1}\in{\cal N}(s)}\theta_{r1,\ldots,r_{k-1}}\prod_{j=1}^{k-1}\phi_{r_{j}}(X_{r_{j}}), \label{eq:eq4} \end{equation}\]onde \(\theta_{s}.:=\{\theta_{s},\theta_{s,r},\cdot\cdot\cdot,\theta_{s r_{2}\ldots r_{k}}\}\) é um conjunto de parâmetros e \(N(s)\) é o conjunto de vizinhos dos vértices conforme o grafo \(G\). Fatorar \(p\) distribuições condicionais fornece a seguinte distribuição conjunta
\[P(X)=\exp\left\{\sum_{s\in V}\theta_{s}\phi_{s}(X_{s})+\sum_{s\in V}\sum_{r\in N(s)}\theta_{s,r}\phi_{s}(X_{s})\phi_{r}(X_{r})+\right.\]
\[\begin{equation} \cdot\cdot\cdot+\sum_{r_{1},...,r_{k}\in{\cal C}}\theta_{r_{1},...,r_{k}}\prod_{j=1}^{k}\phi_{r_{j}}(X_{r_{j}})+\sum_{s\in V}B_{s}(X_{s})-\Phi(\theta)\Bigg\}\,, \label{eq:eq5} \end{equation}\]onde \(\Phi(\theta)\) é a constante de normalização logarítmica.
A dimensionalidade do vetor de parâmetros \(\theta\) depende tanto do tipo de variáveis modeladas quanto da ordem das interações. Se modelarmos apenas variáveis contínuas com interações pares \((k = 2)\), o MGM simplifica para a distribuição gaussiana multivariada que é parametrizada por um vetor \(1\) x \(p\) de interceptações e uma matriz \(p\) x \(p\) de \(\binom{p}{2}\) correlações parciais. Incluir todas as interações trilaterais levaria a um adicional \(\binom{p}{3}\) parâmetros, etc.
As condições necessárias para que a função de densidade mista seja normalizável. Neste artigo Selection and Estimation for Mixed Graphical Models, os autores identificam restrições no espaço de parâmetros necessárias para a existência de uma densidade conjunta bem definida. Essas restrições são importantes para garantir a normalização em uma série de Modelos Gráficos Mistos (MGMs) com, no máximo, interações entre pares.
Os autores também estabelecem a consistência da abordagem de seleção de vizinhança para a reconstrução do grafo em altas dimensões quando o grafo subjacente verdadeiro é esparso. Isso é motivado pelos resultados teóricos, onde eles investigam a seleção de arestas entre nós cujas distribuições condicionais assumem diferentes formas paramétricas. Além disso, eles demonstram que a eficiência pode ser obtida se as estimativas de arestas obtidas das regressões de nós particulares forem usadas para reconstruir o gráfico.
Exemplo: O modelo Ising-Gaussiano
Seja o modelo Ising-Gaussiano como um exemplo específico da distribuição conjunta. Considere um vetor aleatório \(X:= (Y,Z)\), onde \(Y={Y_{1},...,Y_{p1}}\) são variáveis aleatórias gaussianas univariadas, \(Z={Z_{1},...,Z_{p2}}\) são variáveis aleatórias univariadas de Bernoulli e consideramos apenas interações pareadas entre estatísticas suficientes. Para a distribuição gaussiana univariada (com variância conhecida \(\sigma^2\)) a função estatística suficiente é \(\phi_{Y}(Y_{s})=\frac{Y_{s}}{\sigma_{s}}\) e a medida básica é \(B_{Y}(Y_{s})\,=\,-\frac{Y_{s}^{2}}{2\sigma_{s}^{2}}\). A distribuição de Bernoulli tem função estatística suficiente \(\phi_{Z_{s}} = Z_{s}\) e a medida base \(B_{Z}(Z_{s}) = 0\). Da distribuição conjunta MGM segue-se que esta densidade mista é dada por
\[P(Y,Z)\propto\exp\Biggr\{\sum_{s\in V_{Y}}{\frac{\theta_{s}}{\sigma_{s}}}Y_{s}+\sum_{r\in V_{Z}}\theta_{r}Z_{r}+\sum_{(s,r)\in E_{Y}}{\frac{\theta_{s,r}}{\sigma_{s}\sigma_{r}}}Y_{s}Y_{r}+\]
\[\sum_{(s,r)\in E_{\mathrm{Z}}}\theta_{s,r}Z_{s}Z_{r}+\sum_{(s,r)\in E_{\mathrm{YZ}}}\frac{\theta_{s,r}}{\sigma_{s}}Y_{s}Z_{r}-\sum_{s\in V_{\mathrm{Y}}}\frac{Y_{s}^{2}}{2\sigma_{s}^{2}}\Biggr\}\]
onde os dois primeiros termos são limites para variáveis gaussianas e de Bernoulli, o terceiro termo representa interações pareadas entre variáveis gaussianas, o quarto termo representa interações pareadas entre variáveis Bernoulli, o quinto termo representa interações pareadas entre variáveis gaussianas e Bernoulli e o último termo soma sobre o medidas básicas para os gaussianos.
Quando a distribuição condicional é uma variável aleatória de Bernoulli \(Z_{r}\), ela é dada por
\[\begin{equation} P(Z_{r}|Z_{\backslash r}\ ,Y)\propto\exp\left\{\theta_{r}Z_{r}+\sum_{s\in N(r)_{Z}}\theta_{s,r}Z_{s}Z_{r}+\sum_{s\in N(r)_{Y}}\frac{\theta_{s,r}}{\sigma_{r}}Z_{r}Y_{s}\right\}. \label{eq:eq6} \end{equation}\]Observe que a distribuição condicional tem a mesma forma que a distribuição de uma única variável condicionada a todas as variáveis restantes em um modelo de Ising mais um termo adicional para interações entre variáveis aleatórias Bernoulli e Gaussianas.
Quando a distribuição condicional é uma variável aleatória gaussiana \(Y_{s}\), ela é dada por
\[P(Y_{s}|Y_{\backslash s},Z)\propto\exp\left\{{\frac{\theta_{s}}{\sigma_{s}}}Y_{s}+\sum_{r\in{\cal{N}}(s)_{Y}}{\frac{\theta_{s,r}}{\sigma_{s}\sigma_{r}}}Y_{s}Y_{r}+\sum_{r\in{\cal{N}}(s)_{Z}}{\frac{\theta_{s,r}}{\sigma_{s}}}Y_{s}Z_{r}-{\frac{Y_{s}^{2}}{2\sigma_{s}^{2}}}\right\}.\]
Agora, seja \(\sigma=1\), fatore \(Y_{s}\) e seja \(\mu_{s}=\theta_{s}+\sum_{r\in{\cal N}(s)_{Y}}\theta_{s,r}Y_{r}+\sum_{r\in{\cal N}(s)_{Z}}\theta_{s,r}Z_{r}\). Finalmente, ao tomar \(\frac{\mu_{s}^{2}}{2}\) fora da constante de normalização logarítmica, chegamos com álgebra básica à forma bem conhecida da distribuição gaussiana univariada com variância unitária
\[P(Y_{s}|Y_{\backslash s},Z)={\frac{1}{\sqrt{2\pi}}}\exp\left\{-{\frac{(Y_{s}-\mu_{s})^{2}}{2}}\right\}.\]
Relação entre parâmetros do modelo e arestas no grafo
Para MGMs pareados (ou seja, o tamanho dos cliques é no máximo \((k = 2)\)), uma interação pareada entre duas variáveis contínuas \(s\) e \(r\) é parametrizada por um único parâmetro \(\theta_{s,r}\). Agora, se a aresta entre \(s\) e \(r\) presente depende de \(\theta_{s,r}\) que seja ou não zero, ou seja, \((s,r) \in E \Leftrightarrow \theta_{s,r} \neq 0\). Assim, se apenas interações pareadas entre variáveis contínuas são modeladas, qualquer aresta dada é uma função de um único parâmetro. Isso implica que um grafo ponderado representa completamente a parametrização das interações no modelo subjacente (ou a parametrização completa subtraindo os parâmetros de limiar). Interações entre variáveis categóricas com \(m > 2\), no entanto, são especificadas por mais de um parâmetro. Por exemplo, uma interação pareada entre duas variáveis categóricas com \(m\) e \(u\) categorias é parametrizada por \(R = (m - 1) \times (u - 1)\) parâmetros associados às funções de indicador correspondentes para todos os estados \(R\).
Uma interação pareada entre uma variável categórica com \(m\) categorias e uma variável contínua tem \(R = 1 \times (m - 1)\) parâmetros associados com \(m - 1\) funções indicadoras multiplicadas pela variável contínua. Neste caso, \(\theta_{s,r}^z\) é um parâmetro que define a interação entre os nós \(s\) e \(r\) indexados por \(z \in \{1,...,R\}\). Uma aresta está presente entre \(s\) e \(r\) se todos os parâmetros não têm o mesmo valor, indicando que nem todos os estados têm a mesma probabilidade. No MGM usamos a parametrização para regressão multinomial em glmnet, que modela a probabilidade de cada estado da variável prevista, e codifica a primeira categoria da variável preditora como a categoria de referência que é absorvida no intercepto. Isso resulta em \(m \times (u - 1)\) parâmetros, onde \(m\) indica o número de categorias da variável prevista. Nesta parametrização, uma aresta está presente se qualquer um dos parâmetros em \(\theta_{sr}\) são diferentes de zero, ou seja, \((s,r) \in E \Leftrightarrow \exists r : |\theta_{s,r}^z| > 0\). Portanto, dependendo de quais variáveis uma aresta conecta, ela é definida com relação a um ou vários parâmetros.
Para MGMs de ordem \(k\) geral, uma aresta entre os nós \(s\) e \(r\) é uma função de todos os cliques de tamanho até \(k\) que incluem ambos \(s\) e \(r\). Portanto, por exemplo, não é claro a partir do grafo \(G\) se a aresta \((s,r)\) é devida a uma interação entre pares ou a interações de ordem superior (cliques) que inclui \(s\) e \(r\), ou ambas. O número de parâmetros associados a cada clique discutido acima para interações entre pares se estende a interações de ordem \(k\). Uma interação entre \(k\) variáveis contínuas é parametrizada por um único parâmetro \(\theta_{r1,...,rk-1}\) e uma interação entre variáveis categóricas é parametrizada por \((m_{1}-1)\times ... \times (m_{k}-1)\) parâmetros, onde \(m_{1}, m_{2},..., m_{k}\) são o número de categorias de cada variável categórica. Nesta monografia nos concentramos principalmente na estimativa de MGMs pareados, onde cada aresta é uma função do(s) parâmetro(s) de uma única interação pareada.
Estimando modelos gráficos mistos
Nesta seção, discutimos como estimar os parâmetros de uma distribuição conjunta da forma a partir do conjunto de dados. O modelo gráfico \(G\) é então obtido a partir das estimativas dos parâmetros conforme discutido na seção anterior.
Sabemos que a distribuição conjunta pode ser representada como uma fatoração de distribuições condicionais univariadas. Assim, se estimarmos as distribuições condicionais \(p\) univariadas com a parametrização, obtemos a distribuição conjunta. Como todas as distribuições condicionais univariadas são membros da família exponencial, é possível estimar a distribuição conjunta por uma série de \(p\) regressões na estrutura do modelo linear generalizado (GLM). Do ponto de vista dos modelos gráficos, isso significa que estimamos a vizinhança \(N(s)\) de cada nó \(s \in V\) e então combinamos todas as vizinhanças para obter uma estimativa do gráfico \(G\).
Para obter estimativas de parâmetros que sejam exatamente zero (e, portanto, impliquem ausência de arestas no grafo), minimizamos a log-verossimilhança \(\mathcal{L}(\theta,X)\) juntamente com a norma \(\ell_{1}\) do vetor de parâmetro
\[\begin{equation} \hat{\theta}=\arg\operatorname*{min}_{\theta}\left\{-\mathcal{L}(\theta,X)+\lambda\|\theta\|_{1}\right\}, \label{eq:eq7} \end{equation}\]onde \(||\theta||_{1}=\sum_{j=1}^{J}|\theta_{j}|\), \(J\) é o tamanho do vetor de parâmetros \(\theta\) e \(\lambda\) é uma regularização paramêtrica que determina os pesos relativos da log-verossimilhança e da norma \(\ell_{1}\) do vetor de parâmetros. A log-verossimilhança \(\mathcal{L}(\theta,X)\) é definida em relação à família exponencial da distribuição do nó em questão. No caso gaussiano, minimizando a log-verossimilhança negativa é equivalente a minimizar a perda quadrática \(-\mathcal{L}(\theta,X) = ||X_{s}-X_{\backslash s}\theta||_{2}^{2}\). Em outras palavras, estamos perfomando uma regressão LASSO \(\ell_{1}\) penalizada na estrutura GLM com uma função de link apropriado para o nó em questão. A penalização \(\ell_{1}\) garante que o modelo é identificado no cenário de alta dimensão \(p > n\), onde temos mais parâmetros do que observações.
A matriz de desenho é definida em relação à distribuição condicional dos nós no MGM de ordem k. Por exemplo, se \(k = 2\), a matriz de desenho para a regressão no nó \(s\) contém todos outras variáveis ou as funções indicadoras correspondentes (para variáveis categóricas). Se \(k =3\), a matriz de desenho para a regressão no nó \(s\) contém todas as outras variáveis ou as correspondentes funções indicadoras, além dos produtos de todos os pares de variáveis em \(V_{\backslash s}\), ou o \((m - 1) \times (u - 1)\) funções indicadoras no caso de variáveis categóricas com categorias \(m\) e \(u\).
Para dar garantias não assintóticas de taxas positivas falsas e verdadeiras para o \(\ell_{1}\)-regularizado, estimador da regressão, é necessário colocar um limite inferior \(\tau\) no tamanho dos parâmetros no modelo verdadeiro. Esta suposição é frequentemente chamada de condição beta mínima. Ao limitar as estimativas em \(\tau\), aplicamos aproximadamente esta condição. Para estimar a distribuição conjunta utiliza-se da seguinte condição
\[\begin{equation} \tau \asymp s_{0}\sqrt{\log\frac{p}{n}}\le s_{0}\lambda, \label{eq:eq8} \end{equation}\]onde \(s_{0}\) é o verdadeiro número de vizinhos. Se todas as variáveis forem contínuas, o número de vizinhos é igual ao número de estimativas de parâmetros diferentes de zero \(s_{0}=||\theta^*||_{0}\), onde \(\theta^*\) é o vetor de parâmetros verdadeiro. No caso de variáveis categóricas, as interações são parametrizadas por vários parâmetros. Neste caso o vizinho categórico está presente se pelo menos um dos parâmetros que definem a interação são diferentes de zero. Como o verdadeiro vetor de parâmetros \(\theta^*\) é desconhecido, substituímos o vetor de parâmetros estimado \(\hat{\theta}\) para obter o número estimado de vizinhos \(\hat{s}_{0}= ||\theta^*||_{0}\). Para interações envolvendo mais de um parâmetro, inserimos o valor agregado parâmetro.
Determinamos se uma aresta está presente ou não conforme. Além disso, calculamos um peso a partir do conjunto de parâmetros de cada interação. Se a interação apenas envolve variáveis contínuas, existe apenas um parâmetro e tomamos seu valor. Se a interação envolve variáveis categóricas, tomamos a média do valor absoluto de todos os parâmetros como o peso da aresta. A partir das regressões nodais, obtemos \(k\) pesos de aresta para cada interação de ordem \(k\). Por exemplo, para uma interação de pares (\(k = 2\)) entre os nós \(s\) e \(r\), obtemos um parâmetro \(\theta_{s,r}\) da regressão em \(s\) e \(\theta_{r,s}\) da regressão em \(r\). Para obter um grafo de dependência condicional final \(G\), precisamos combiná-los em um peso final. Isso pode ser feito usando a regra OR (faça a média aritmética das estimativas de k parâmetros) ou a regra AND (tome a média aritmética de k estimativas de parâmetros se todas as estimativas de parâmetros são diferentes de zero, caso contrário, defina o parâmetro como zero).
O algoritmo a seguir resume o processo:
Algoritmo (Estimando modelos gráficos mistos por meio de regressão de vizinhança.)
Para cada \(s\in V\) :
- Construa a matriz de projeto definida por k, a ordem do MGM.
- _Resolva o problema do lasso com parâmetro de regularização \(\lambda.\)
- Limite as estimativas em \(\tau.\)
- Agregue interações com vários parâmetros em um único peso de aresta.
Combine os pesos das arestas com a regra AND ou OR.
Defina \(G\) com base no padrão zero/diferente de zero no vetor de parâmetros combinados.
O parâmetro de regularização \(\lambda\) pode ser selecionado usando validação cruzada ou seleção de modelo critério como o critério de informação Bayesiano estendido (EBIC):
\[\begin{equation} EBIC_{\gamma} = -2\mathcal{L}(\hat{\theta}) + s_{0}\log{n} + 2\gamma\hat{s}_{0}\log{p}, \label{eq:eq9} \end{equation}\]onde \(\mathcal{L}\) é a log-verossimilhança da função de densidade condicional dada pelo vetor de parâmetros estimado \(\theta\); \(s_{0}\) é o número de vizinhos diferentes de zero no modelo candidato e \(\gamma\) é um parâmetro de ajuste. Perceba que se \(\gamma = 0\) o EBIC se torna equivalente ao BIC. O EBIC demonstrou ter um bom desempenho assintoticamente na seleção de grafos esparsos para qualquer valor de \(\gamma\). Na prática, a escolha do valor de \(\gamma\) controlará o trade-off entre sensibilidade e precisão.
A complexidade computacional do algoritmo é \(\mathcal{O}(p\log(p2^{k-1}))\). Assim o algoritmo faz não performa bem para um valor de \(k\) grande, sendo \(k\) a ordem das interações no MGM. Contudo, na maioria das situações \(k\) será pequeno, porque as interações com ordem superior são cada vez mais difíceis de interpretar e, portanto, muitas vezes não é de interesse.
Observe que usar um único parâmetro de regularização \(\lambda\) para um modelo incluindo diferentes tipos de arestas pode levar a uma penalização diferente para diferentes tipos de arestas. Isso ocorre porque os parâmetros de borda do grafo são dimensionados com a estatística suficiente à qual estão associados e esse dimensionamento pode diferir entre membros da família exponencial. Embora possamos trazer variáveis gaussianas na mesma escala subtraindo sua média e dividindo pelo seu desvio padrão, isso não é possível para variáveis aleatórias categóricas ou de Poisson. Uma solução potencial seria introduzir um sistema diferente parâmetro de penalização para cada tipo de aresta, porém, isso tornaria a seleção da regularização parâmetros \(\lambda\) consideravelmente mais complicados, porque agora um espaço \(u\)-dimensional de valores \(\lambda\) deve ser pesquisado, onde \(u\) é o número de diferentes tipos de arestas. É por isso que atualmente não possui um procedimento no mgm que permita diferentes penalidades para diferentes tipos de arestas.
O desempenho do Algoritmo depende do número de variáveis, da ordem das interações, do tipo de variáveis, do tamanho dos parâmetros em relação à variância das variáveis associadas, da dispersão do vetor de parâmetros e da estrutura do grafo de dependência. A melhor maneira de determinar o desempenho para uma determinada situação é, portanto, obtê-lo com uma simulação estudada. Para este fim, o mgm fornece uma função flexível para amostras de MGMs, de modo que o o desempenho do Algoritmo em uma determinada situação pode ser avaliado por meio de simulações.
Modelos Gráficos Mistos variantes no tempo
Para o modelo gráfico misto, assumimos que ele é estacionário, ou seja, suas propriedades estatísticas, como média e variância, não mudam ao longo do tempo. Isto significa que as observações em cada ponto \(t\) no tempo são gerados a partir da mesma distribuição parametrizada por \(\theta\). Nos modelos variantes no tempo, assumimos essa suposição, de modo que os parâmetros \(\theta^t\) pode ser diferente a ponto do tempo \(t\in T_{n}=\{\textstyle{\frac{1}{n}},\textstyle{\frac{2}{n}},\dots,1\}\), onde \(n\) é o número de pontos estimados na série temporal. Observe que usamos \(n\) para denotar o número de observações tanto para dados transversais e dados de séries temporais.
Como não se pode estimar um modelo a partir de um único ponto no tempo, temos que fazer suposições sobre como os parâmetros do modelo verdadeiro variam em função do tempo. Essas suposições geralmente são suposições sobre a estacionariedade local, e vem em uma de duas opções: ou assumimos que existe uma partição \({\mathcal{B}}{\mathrm{~of~}}\mathcal{T}_{n}\) em pontos de tempo que são consecutivos e em cada um dos subconjuntos \(B \in \mathcal{B}\) são estacionários, isso é, \(\forall i,j\in B:\theta^{i}=\theta^{j}\). Esses modelos constantes e variantes no tempo por partes podem ser estimados com lasso penalizado fundido, que impõe uma penalidade adicional nas alterações de parâmetro de um ponto no tempo para o ponto no tempo subsequente.
O outro tipo de estacionariedade local, no qual nos concentramos nesta monografia, exige que o modelo \(\theta^t\) é uma função suave do tempo. Neste caso podemos combinar observações próximas no tempo para estimativa, pois sabemos que seus modelos geradores são semelhantes. Esta ideia é implementada ajustando modelos locais \(\theta^{t^e}\) ao longo da série temporal, o que apenas dá grande peso aos dados próximos ao ponto de estimativa dado em \(t^e\). A função peso geralmente é não negativa e simétrica sobre \(t^e\). O modelo completo variante no tempo é então o conjunto de todas as estimativas locais \(\{\theta^{e_{1}},\theta^{e_{2}},\dots,\theta^{|\xi|}\}\) nos pontos estimados \({\mathcal{E}}=\{t_{1}^{e},t_{2}^{e},...,t^{|\mathcal{E}|}\}\) onde as entradas em \(\mathcal{E}\) geralmente são igualmente espaçados ao longo da série temporal e o número de pontos de estimativa \(|\mathcal{E}|\) é escolhido dependendo de como \(\theta^t\) é descrito em função do tempo \(t\).
Estimando modelos gráficos mistos variantes no tempo
Dada a formalização na seção anterior, estimamos o modelo \(\theta^{t^e}\) no momento \(t\) minimizando uma versão ponderada da função de perda:
\[\begin{equation} \hat{\theta}^{t^e}=\arg\mathrm{min}_{\theta}\left\{-\frac{1}{\sum_{t=1}^{n}w_{t}^{t e}}\sum_{t=1}^{n}w_{t}^{t e}\mathcal{L}(\theta,X^{t})+\lambda||\theta||1\right\}, \label{eq:eq11} \end{equation}\]onde \(w_{t}^{t e}\) é uma função de \(t\) definida por um kernel central por \(t^e\). Especificamente, definimos a função de peso \(w_{t}^{t e}\) para ser um kernel gaussiano, normalizado de modo que o maior peso seja igual para um, veja ,
\[\begin{equation} w_{t}^{t e}=\frac{Z_{t}}{\operatorname*{max}_{(t\in T_{n})\;\{\,\cup_{t}Z_{t}\}}},\quad\mathrm{onde}\quad Z_{t}=\frac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\frac{(t-t^{e})^{2}}{2\sigma^{2}}\right\} \label{eq:eq12} \end{equation}\]Esta escala específica da função peso tem a propriedade conveniente de que a soma de todos os pesos \(n_{\sigma,t^{e}}=\sum_{t=1}^{n}w_{t}^{t^{e}}\) (equivalente a área abaixo da curva) usados e dados na estimação do ponto \(t^e\) indicando a quantidade de dados usados para estimativa em \(t^e\) em relação à série temporal completa. Perceba que indexamos \(n_{\sigma,t^{e}}\) também com o ponto estimado \(t^e\), pelo fato de que menos dados são usados no início e no final da série temporal, onde a função de ponderação é truncada.
A largura de banda \(\sigma\) do kernel, que é igual ao desvio padrão da distribuição gaussiana, indica quantas observações próximas no tempo combinamos para estimar o nó no ponto de estimativa \(t^e\).
A escolha da largura de banda envolve um trade-off entre a sensibilidade aos parâmetros que variam com o tempo e a estabilidade das estimativas: se combinarmos apenas algumas observações próximas no tempo (pequena largura de banda \(\sigma\)), o algoritmo pode detectar a variação dos parâmetros em pequenas escalas de tempo. Se combinarmos muitas observações em torno do ponto de estimativa (valor alto para \(\sigma\)), a variação de parâmetros em pequenas escalas de tempo será perdida devido à agregação, no entanto, as estimativas serão relativamente estáveis. Observe que se continuarmos aumentando a largura de banda \(\sigma\), os pesos em [0,1] convergirão para uma distribuição uniforme e darão as mesmas estimativas que a versão estacionária do modelo, tornando-se assim relativamente estáveis, mas perdendo toda a sensibilidade para detectar mudanças nos parâmetros ao longo do tempo.
A largura de banda ideal \(\sigma^*\) resulta no vetor de parâmetros estimado \(\theta^t\) que minimiza a distância para o verdadeiro modelo variante no tempo \(\theta^{t*}\) como uma função de \(\sigma\). Podemos fazer a estimação de \(\sigma^*\) usando um esquema de validação cruzada estratificado no tempo, onde se busca uma sequência \(\sigma\) especificada e seleciona-se o \(\sigma\) que minimiza o erro médio de predição fora da amostra (entre dobras e variáveis).
Vejamos o algoritmo do processo:
Algoritmo (Estimando modelos gráficos mistos variantes no tempo por meio de regressão de vizinhança suavizada pelo kernel.)
Para cada ponto de estimação \(t^e \in \mathcal{E}\) :
Para cada variável \(s \in V\) :
- Construa a matriz de projeto definida por k, a ordem do MGM.
- Resolva o problema do lasso com o parâmetro de regularização \(\lambda\) e com a função de peso \(w^{t^e}\) definida por \(t^e\) e a largura de banda \(\sigma\).
- Limite as estimativas em \(\tau.\)
- Agregue interações com vários parâmetros em um único peso de aresta.
Combine os pesos das arestas com a regra AND ou OR.
Defina \(G^e\) com base no padrão zero/diferente de zero no vetor de parâmetros combinados \(\theta^e\).
Assim obtemos um vetor de parâmetros \(\theta^{t^e}\) do MGM e um vetor de grafos \(G^{t^e}\) definido por \(\theta^{t^e}\) para cada ponto de estimação \(t^e \in \mathcal{E}\).
Centralidade
A centralidade nos ajuda a entender quem são os “atores-chave” em um grafo e como eles afetam a dinâmica geral. Imagine que temos uma rede, como uma teia de conexões entre pessoas, salas em um prédio ou estradas em uma cidade. A centralidade de um vértice (ou nó) nessa rede mede sua importância relativa.
Vejamos nos tópicos a seguir as diferentes centralidades que usaremos nesse trabalho. As formulações referentes ao tema foram adaptadas a partir e .
Centralidade de Grau
Essa medida está relacionada ao número de conexões que um vértice possui. Quanto mais conexões (ou “amigos”), maior a centralidade de grau. Por exemplo, se você tem muitos amigos em uma rede social, seu grau de centralidade é alto.
A centralidade de grau de um vértice é definida como o número de vértices conectados com este vértice por médio de uma aresta que pertence ao grafo:
\[d(i) = \sum_{j:(i,j)\in E}1\]
Centralidade de Grau Temporal
A centralidade de grau temporal é uma medida utilizada em redes temporais para avaliar a importância dos vértices com base em suas conexões ao longo do tempo.
Definida por \(\mathcal{D}_{i,j}(v)\) para um nó \(v \in V\) num intervalo \([i,j]\) onde \(0 \le i < j \le n\) é o número total de arestas de entrada de \(v\) para o intervalo de tempo \([i,j]\) desconsiderando as “auto-arestas” de \(v_{t-1}\) para \(v_{t}\) para todo \(t \in {i+1, ..., j}\). Isto é igual a
\[\sum_{t=i}^j 2 \times \mathcal{D}_{t}(v)\]
onde \({D}_{t}(v)\) é o grau de \(v\) no grafo \(G_{t}\)(grafo no instante t).
O grau temporal pode ser normalizado dividindo cada grau de nó por \(2\times(|V|-1)\times m\) onde \(m=j-i\). Notamos que o grau temporal normalizado de um nó é igual ao valor médio dos valores de grau do nó em a série temporal de gráficos.
Dado um grafo \(G\) ordenado no tempo vindo de \(G_{i}^{\mathcal{D}} = (V, E_{i,j})\), os valores de grau temporal de todos os nós em \(V\) podem ser computados em \(O(|V|+| \mathcal{E} |)\) tempo verificando os nós adjacentes a cada aresta em \(\mathcal{E}\).
Centralidade de Proximidade
Essa medida avalia o quão perto um vértice está de outros vértices na rede. Se você está próximo de muitos outros vértices, sua centralidade de proximidade é alta. Pense nisso como a rapidez com que você pode se comunicar com outras pessoas na rede.
A centralidade de proximidade de um vértice é definida como o inverso da soma das distâncias a todos os outros vértices do gráfico:
\[C_{C}(v) = \frac{1}{\sum_{s \in V} d(s,v)}, v \in V\]
onde \(d(v,u)\) é a distância (número de arestas) da geodésica entre \(s\) e \(v\).
Centralidade de Proximidade Temporal
A centralidade de proximidade temporal mede quão central um nó é em termos de quando ele se comunica com outros nós. Em outras palavras, ela considera a frequência e o tempo das interações de um nó com os demais.
Essa medida, definida por \(\mathcal{C}_{i,j}(v)\) para um nó \(v \in V\) em um intervalo de tempo \([i,j]\) onde \(0 \le i < j \le n\) é a soma das distâncias do caminho mais curto temporal invertido para todos os outros nós em \(V\smallsetminus v\) para cada intervalo de tempo \(\{[t,j]:i\leq t<j\}\). Dessa forma, formalmente, definimos:
\[C_{i,j}(v)=\sum_{i \le t<j}\sum_{u\in V\smallsetminus v}{\frac{1}{\Delta_{t,j}(v,u)}}\]
onde \(\Delta_{t,j}(v,u)\) é a distância temporal mais curta de \(v\) a \(u\) em um intervalo de tempo \([t, j]\).
Centralidade de Mediação
Aqui, olhamos para os caminhos que passam por um vértice. Se um vértice está no meio de muitos caminhos, ele tem alta centralidade de mediação. Isso é como ser um “conector” entre diferentes grupos de pessoas.
A centralidade de mediação de um vértice é definida como a média de todos os caminhos que usam esse vértice:
\[\mathcal{B}(v)=\sum_{s\ne u \ne v \in V}\frac{\sigma(s,t|v)}{\sigma(s,t)},\ \ \ v\in V\] onde \(\sigma(s,t|v)\) é o número de geodésicas entre \(s\) e \(t\) que passam por \(v\) e \(\sigma(s, t)\) é uma constante normalizadora definida por \(\sigma(s,t) = \sum_{v}\sigma(s,t|v)\).
Centralidade de Mediação Temporal
A centralidade de mediação temporal nos ajuda a identificar os nós que desempenham um papel crucial na comunicação entre outros nós ao longo do tempo. Esses nós atuam como intermediários, conectando diferentes partes da rede.
Essa medida, definida por \(\mathcal{B}_{i,j}(v)\) para um nó \(v \in V\) em um intervalo de tempo \([i,j]\) onde \(0 \le i < j \le n\) é a soma da proporção de todos os caminhos mais curtos temporais através do vértice \(V\) com o número total de caminhos mais curtos temporais sobre todos os pares de nós para cada intervalo de tempo em \(\{[t,j]:i\leq t<j\}\). Dessa forma, formalmente, definimos:
\[\mathcal{B}_{i,j}(v)=\sum_{i\leq t<j}\sum_{s\neq v\neq d\in V }{\frac{\sigma_{t,j}(s,d,v)}{\sigma_{t,j}(s,d)}}\] onde \(\sigma_{t,j}(s,d) \equiv |\mathcal{S}_{t,j}(s,d)|\) e \(\sigma_{t,j}(s,d,v) \equiv |\mathcal{S}_{t,j}(s,d,v)|\).
Problematização
A aplicação de um modelo gráfico misto variante no tempo em uma base de dados de prêmios e sinistros, abrangendo o período de 2001 a 2023, envolve considerações importantes. Vamos explorar os aspectos relevantes dessa problemática:
- Base de Dados de Prêmios e Sinistros
A base de dados1000000 contém informações sobre prêmios (receitas) e sinistros (pagamentos de indenizações) ao longo de mais de duas décadas. Esses dados podem ser complexos, com diferentes tipos de variáveis (contínuas, discretas, categóricas) e alta dimensionalidade.
- Modelo Gráfico
Os modelos gráficos são ferramentas poderosas para representar relações entre variáveis. O modelo gráfico misto é uma extensão que permite lidar com diferentes tipos de variáveis em um único framework. Ele captura dependências entre variáveis e ajuda a entender a estrutura subjacente dos dados.
- Variação Temporal
A variação temporal é crucial em dados financeiros, como prêmios e sinistros. O uso de um modelo gráfico misto com variação temporal permite capturar mudanças nas relações entre variáveis ao longo do tempo. Isso é especialmente relevante para entender como eventos externos (por exemplo, mudanças regulatórias, crises econômicas) afetam a dinâmica dos prêmios e sinistros.
Vantagens de se utilizar o Modelo Gráfico Misto com Variação Temporal:
- Flexibilidade
O modelo gráfico misto pode lidar com diferentes tipos de variáveis (por exemplo, contínuas, categóricas) em uma única estrutura. A variação temporal permite que o modelo se adapte a mudanças nas relações ao longo do tempo.
- Identificação de Influências Externas
Com a variação temporal, podemos identificar como eventos externos afetam a estrutura do modelo. Por exemplo, podemos investigar como uma nova política regulatória impacta os prêmios e sinistros.
- Análise de Causalidade
O modelo gráfico misto com variação temporal permite explorar relações de causalidade entre variáveis. Podemos investigar se mudanças nos prêmios causam mudanças nos sinistros ou vice-versa.
Resultados e Discussões Esperados:
- Estrutura de Dependência
O modelo revelará as relações entre prêmios e sinistros. Identificaremos quais variáveis estão mais fortemente conectadas e como essas conexões mudam ao longo do tempo.
- Impacto de Eventos Externos
Analisaremos como eventos específicos (por exemplo, crises financeiras, mudanças regulatórias) afetam a dinâmica dos prêmios e sinistros. Isso pode levar a insights sobre estratégias de gestão de risco.
- Validação e Interpretação
Validaremos o modelo usando técnicas como validação cruzada. Interpretaremos os resultados para comunicar insights relevantes aos stakeholders.
Em resumo, o uso desse modelo nos permitirá entender melhor as relações entre prêmios e sinistros, considerando a complexidade dos dados e as mudanças ao longo do tempo.
Além disso, observaremos características estruturais dos grafos gerados, mais especificamente as centralidades de grau, proximidade e mediação, que nos permitirão entender a estrutura da rede do conjunto de variáveis de prêmios e sinistros.
Dados
Os dados utilizados na análise de Prêmios e Sinistros foram extraídos do site do Sistema de Estatística da SUSEP (SES). Os dados do SES são extraídos dos Formulários de Informações Periódicas (FIP) enviados à SUSEP pelas companhias do setor.
Esses dados são extremamente úteis para entender o desempenho financeiro das seguradoras, a frequência e o custo dos sinistros. Eles também podem ajudar a identificar tendências e padrões no setor de seguros.
Ademais, foi selecionado uma amostra referente ao período de 2001 a 2023 de empresas e ramos que estão presentes desde o início até o fim desse período, mais especificamente, uma amostra de 436499 observações e 17 variáveis. A base de dados utilizada na análise contém informações das seguintes variáveis:
Ramo: código do ramo no FIP;
Prêmio Direto: Refere-se ao valor total dos prêmios recebidos pelas seguradoras diretamente dos segurados durante o período de vigência dos contratos de seguro;
Prêmio de Seguros: É o valor dos prêmios relacionados especificamente aos contratos de seguro. Isso exclui outros tipos de receitas, como investimentos;
Prêmio Retido: Representa a parte do prêmio que a seguradora mantém após deduzir as comissões pagas aos corretores e outras despesas;
Prêmio Ganho: Refere-se à parcela do prêmio que a seguradora reconhece como receita durante o período de vigência do contrato de seguro;
Sinistros de Seguros: São os valores pagos pelas seguradoras aos segurados em decorrência de eventos cobertos pelas apólices de seguro.
Sinistro Retido: Representa a parte dos sinistros que a seguradora assume após deduzir as despesas com resseguro;
Custo de Aquisição: Refere-se aos custos incorridos pelas seguradoras para adquirir novos contratos de seguro, como comissões de corretores e despesas de marketing;
Prêmios Emitidos: São os prêmios totais emitidos pelas seguradoras, incluindo os prêmios diretos e os prêmios cedidos a resseguradoras;
Prêmios Emitidos em Regime de Capitalização: Relacionam-se aos prêmios de seguros emitidos no contexto de planos de capitalização;
Despesa com Resseguros: Refere-se aos custos associados à transferência de riscos para resseguradoras;
Receita com Resseguros: É a receita obtida pelas seguradoras ao ceder parte dos riscos a resseguradoras;
Sinistros Ocorridos: Representam os valores pagos pelas seguradoras em decorrência de sinistros ocorridos durante o período de vigência das apólices;
Sinistros Ocorridos em Regime de Capitalização: Relacionam-se aos sinistros ocorridos em planos de capitalização;
RVNE (Prêmios de Riscos Vigentes e Não Emitidos): corresponde a uma parcela estimada da PPNG (Provisão de Prêmios Não Ganhos) referente a riscos cuja vigência já tenha se iniciado, mas cuja emissão ainda não tenha ocorrido123. Detalhamento:
Riscos Vigentes: São os contratos de seguro que já estão em vigor, ou seja, cuja cobertura já começou a valer, mas que ainda não foram oficialmente emitidos (ou seja, ainda não tiveram o prêmio registrado);
Não Emitidos: Refere-se aos riscos que ainda não tiveram a emissão formal do contrato de seguro, mesmo que a vigência já tenha iniciado.
Recuperação de Sinistros (Regime de Capitalização e Repartição de Capitais de Cobertura): a recuparação de sinistros, no regime de repartição, a solidariedade entre os contribuintes prevalece, e os sinistros são pagos com base na contribuição de todos. Já no regime de capitalização, cada segurado tem sua própria reserva individual, e os sinistros são pagos com base nessa reserva;
Prêmios Convênio DPVAT: Refere-se aos prêmios relacionados ao seguro obrigatório de danos pessoais causados por veículos automotores terrestres (DPVAT).
Para o desenvolvimento das análises e tratamento dos dados, foi utilizado o R, disponível para download em http://www.r-project.org/.
Implementação e Resultados
Modelo Gráfico Misto Variante no Tempo no contexto de Prêmios e Sinistros
O objetivo da aplicação do modelo ao contexto de Prêmios e Sinistros é entender como cada variável se afeta ao longo do tempo, a fim de entender padrões complexos no conjunto de dados de prêmios e sinistros.
A estimação foi feita utilizando interação de pares com \(k = 2\), ou seja, interagindo as variáveis par a par estimando por vizinhança para cada instante \(t\) (23 ao todo, visto que se trata de um período de 23 anos), além de utilizar a regra OR (média aritmética da estimativa de k parâmetros) e uma largura de banda ótima estimada de 0,1 (desvio padrão \(\sigma^*\) da densidade da Normal). Para a chegar a ao valor “ótimo” para a largura de banda foi um feito um trade-off com a base de dados com 5 “dobras” na validação cruzada e tamanho 5, também, em cada dobra.
Vale destacar que o método de estimação de interações entre as variáveis foi feito via modelos lineares generalizado. Para o desenvolvimento do mesmo foi utilizado o R, mais especificamente utilizando a livraria mgm que utiliza como dependência o pacote glmnet em suas interações.
As imagens a seguir possuem a representação gráfica do modelo estimado em cada um dos 23 instantes de tempo.
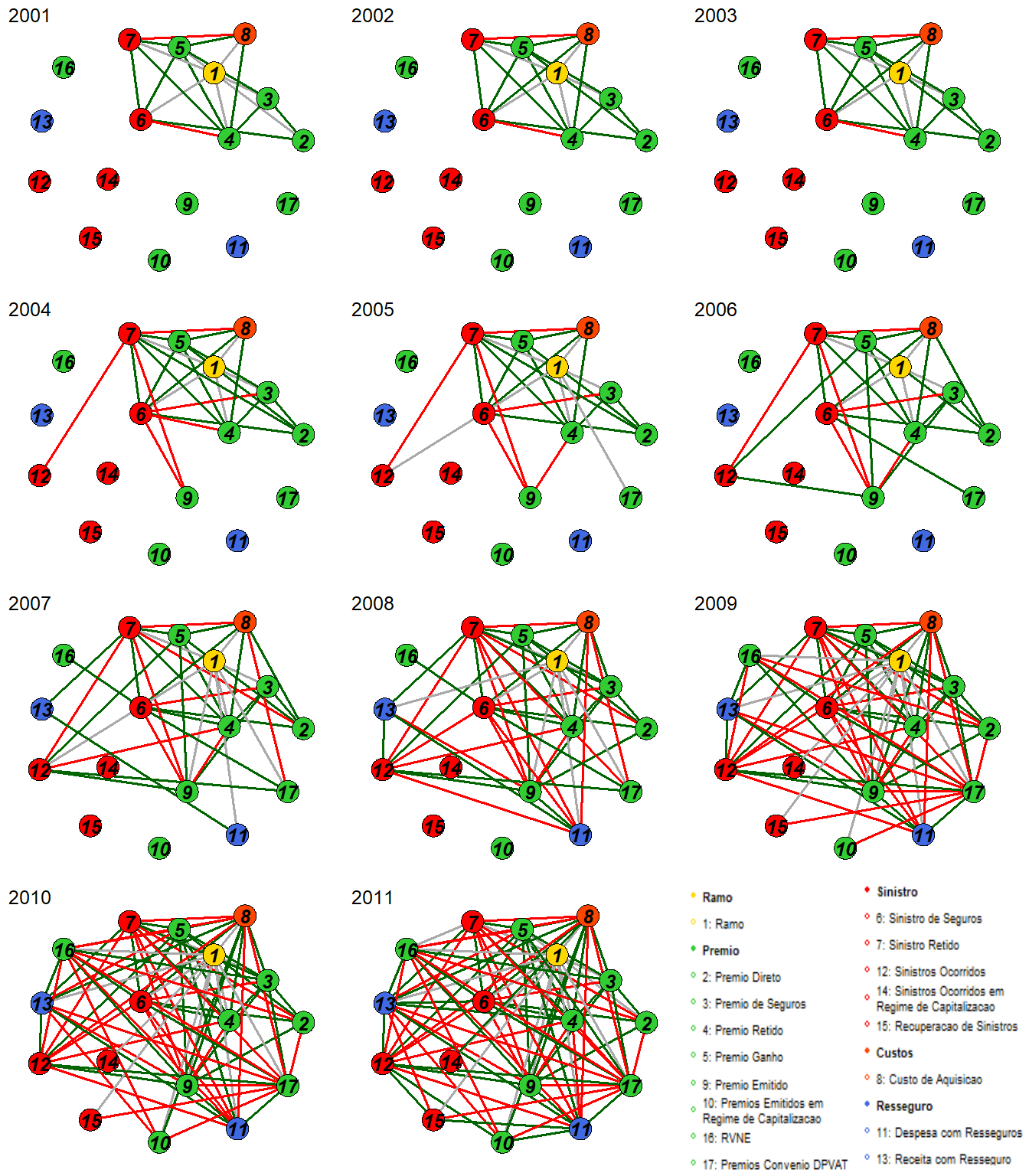
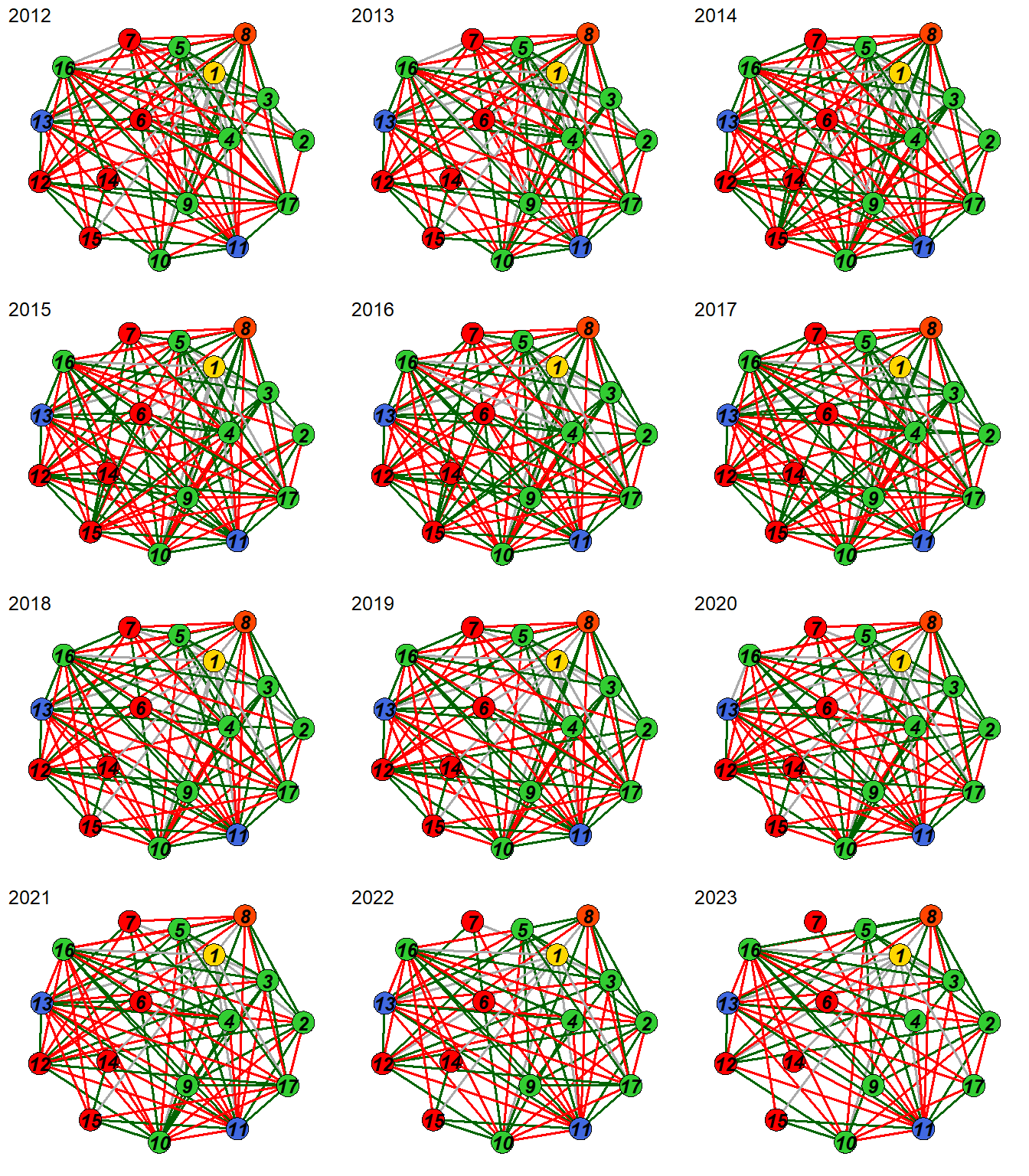
Arestas verdes indicam relacionamentos positivos, arestas vermelhas indicam relacionamentos negativos e arestas cinzas indicam relacionamentos envolvendo variáveis categóricas para as quais nenhum sinal é definido. A largura das bordas é proporcional ao valor absoluto da relação entre as variáveis.
Analisaremos, separadamente, os instantes de tempo , a fim de entender detalhadamente as relações desse grafo. Antes de partirmos para isso, definimos os seguintes itens referentes aos pesos calculados entre as variáveis.
Magnitude dos Pesos: A magnitude dos pesos indica a força da associação entre as variáveis. Pesos maiores (em valor absoluto) indicam associações mais fortes.
Sinal dos Pesos: O sinal dos pesos pode indicar a direção da associação. Por exemplo, um peso positivo pode sugerir uma associação positiva, enquanto um peso negativo pode sugerir uma associação negativa.
- Representação Gráfica do Modelo no Instante de tempo 1:
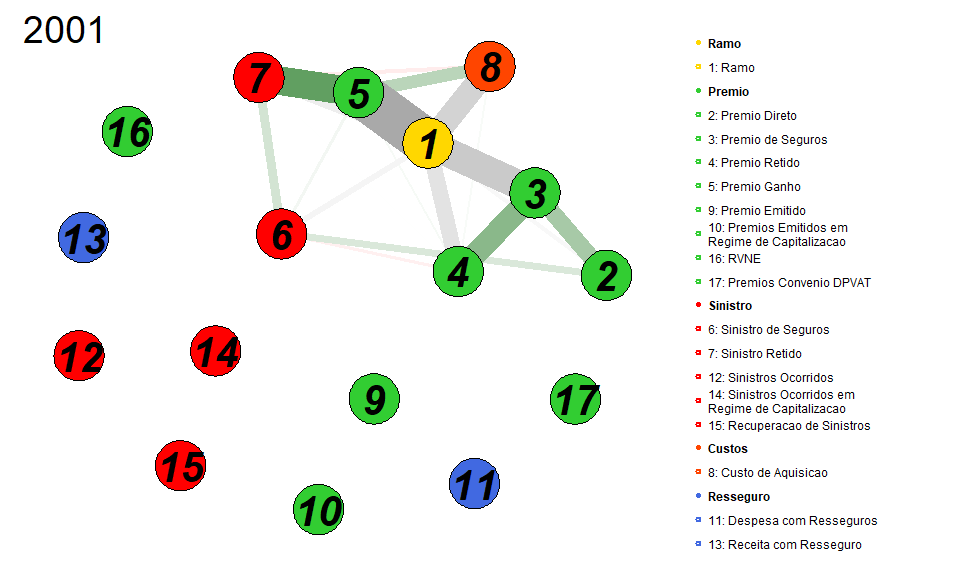
| Variavel 1 | Variavel 2 | Peso |
|---|---|---|
| Premio Direto | Premio de Seguros | 0,814 |
| Premio Direto | Sinistro de Seguros | 0,346 |
| Premio Ganho | Custo de Aquisicao | 0,633 |
| Premio Ganho | Sinistro Retido | 1,462 |
| Premio Ganho | Sinistro de Seguros | 0,114 |
| Premio Retido | Custo de Aquisicao | 0,067 |
| Premio Retido | Premio Ganho | 0,082 |
| Premio Retido | Sinistro Retido | 0,005 |
| Premio Retido | Sinistro de Seguros | 0,139 |
| Premio de Seguros | Premio Ganho | 0,011 |
| Premio de Seguros | Premio Retido | 1,079 |
| Ramo | Custo de Aquisicao | 1,197 |
| Ramo | Premio Direto | 0,194 |
| Ramo | Premio Ganho | 2,355 |
| Ramo | Premio Retido | 0,779 |
| Ramo | Premio de Seguros | 1,442 |
| Ramo | Sinistro Retido | 0,459 |
| Ramo | Sinistro de Seguros | 0,271 |
| Sinistro Retido | Custo de Aquisicao | 0,178 |
| Sinistro de Seguros | Sinistro Retido | 0,405 |
Analisando-se o grafo podemos perceber uma forte relação positiva entre Prêmio Ganho e Sinistro Retido no ano de 2001. Além disso, a variável Ramo apresenta, também, forte relação com Prêmio Ganho.
Demais relações em pesos dos outros instantes de tempo do modelo MGM estarão presentes no anexo desta monografia.
Centralidades Temporais no contexto de Prêmios e Sinistros
A centralidade é uma medida importante em teoria dos grafos que determina a importância de um vértice dentro de um grafo. Exemplos de medidas de centralidade incluem centralidade de grau, proximidade e intermediação/mediação.
No entanto, quando lidamos com grafos temporais, a situação muda um pouco. Grafos temporais são grafos onde as arestas têm informações de tempo associadas a elas. Isso significa que a conexão entre dois vértices não é constante ao longo do tempo, mas pode mudar. Isso é particularmente relevante quando estamos analisando redes dinâmicas ou um período longo de tempo.
Nesse contexto, as medidas de centralidade tradicionais podem não ser suficientes, pois elas não levam em consideração a dimensão temporal. Por exemplo, um vértice pode ter um alto grau de centralidade em um determinado momento, mas um baixo grau em outro. Da mesma forma, a proximidade ou a intermediação de um vértice pode mudar ao longo do tempo.
É aqui que as centralidades temporais entram em jogo. As centralidades temporais levam em consideração a dimensão temporal. Elas permitem analisar como as características estruturais de um vértice mudam ao longo do tempo, o que pode fornecer insights mais profundos sobre a estrutura e a dinâmica da rede.
Veremos a seguir diferentes medidas de centralidades aplicadas as conexões estimadas pelo MGM variante no tempo referente ao universo de variáveis no contexto de prêmios e sinistros. A aplicação se deve ao fato de que essas conexões provavelmente mudam ao longo do tempo, por exemplo, devido a mudanças nas políticas de seguro, no comportamento dos segurados, ou em resposta a eventos externos. Portanto, faz sentido usar centralidades temporais para capturar essas mudanças dinâmicas.
Todos os cálculos foram feitos utilizando o software R com a livraria TNC.
Centralidade de Grau Temporal
O objetivo principal desta centralidade é analisar como a importância de um vértice muda ao longo do tempo em um grafo temporal.
Vejamos a seguir os valores de centralidade de grau temporal de cada uma das variáveis dos grafos estimados pelo MGM variante no tempo representados na visualização a seguir.
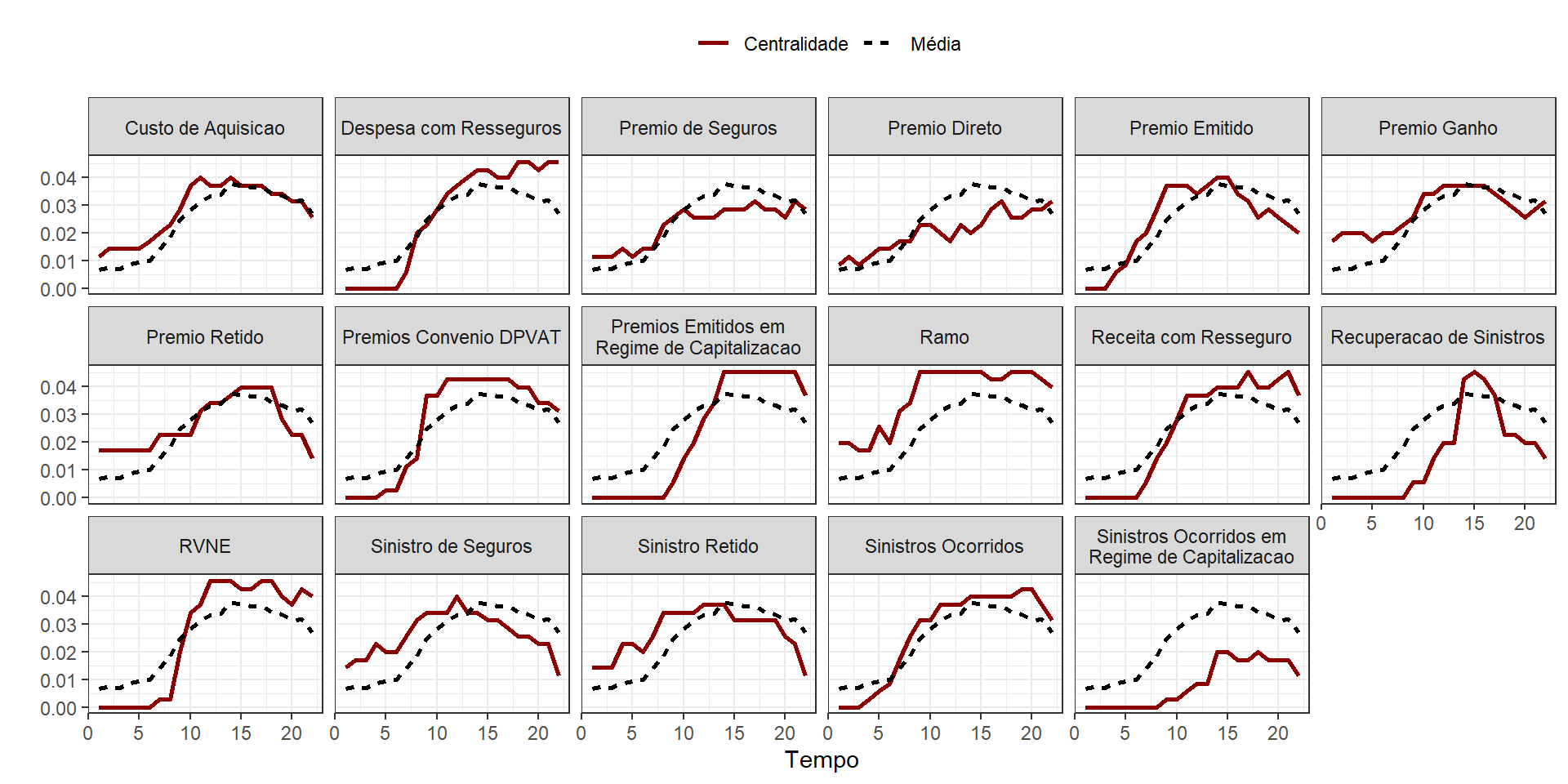
A linha vermelha sólida representa a centralidade temporal específica para cada variável, enquanto a linha preta tracejada representa a média de todas as centralidades ao longo do tempo. Vamos analisar cada subgráfico individualmente.
Custo de Aquisição: A centralidade começa baixa, aumenta até cerca do tempo 10 e depois diminui ligeiramente. A linha média está geralmente acima da centralidade específica, indicando que “Custo de Aquisição” tem uma centralidade menor que a média.
Despesa com Resseguro: A centralidade aumenta rapidamente até o tempo 5, estabiliza e diminui após o tempo 15. A linha média está abaixo da centralidade específica, sugerindo que “Despesa com Resseguro” é mais central do que a média.
Prêmio de Seguros: A centralidade aumenta gradualmente até o tempo 15 e depois estabiliza. A linha média está abaixo da centralidade específica, indicando alta centralidade para “Prêmio de Seguros”.
Prêmio Direto: A centralidade mostra um aumento rápido até o tempo 10, depois estabiliza. A linha média está abaixo da centralidade específica, sugerindo que “Prêmio Direto” também é mais central que a média.
Prêmio Emitido: A centralidade aumenta rapidamente até o tempo 10 e depois começa a diminuir. A linha média está geralmente abaixo da centralidade específica, mostrando alta centralidade relativa.
Prêmio Ganho: A centralidade aumenta até o tempo 15 e depois estabiliza. A linha média está abaixo da centralidade específica, indicando que “Prêmio Ganho” é mais central.
Prêmio Retido: A centralidade mostra um aumento e uma queda abrupta em torno do tempo 5, depois estabiliza. A linha média é geralmente mais alta, indicando que “Prêmio Retido” tem centralidade menor.
Prêmios Convênio DPVAT: A centralidade aumenta até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica, mostrando alta centralidade.
Prêmios Emitidos em Regime de Capitalização: A centralidade aumenta rapidamente até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica.
Ramo: A centralidade aumenta gradualmente e estabiliza após o tempo 10. A linha média está abaixo da centralidade específica, sugerindo alta centralidade.
Receita com Resseguro: A centralidade aumenta até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica.
Recuperação de Sinistros: A centralidade aumenta rapidamente até o tempo 10 e depois diminui. A linha média está acima da centralidade específica, indicando menor centralidade.
RVNE: A centralidade aumenta rapidamente até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica.
Sinistro de Seguros: A centralidade aumenta rapidamente até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica.
Sinistro Retido: A centralidade aumenta até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica.
Sinistros Ocorridos: A centralidade aumenta rapidamente até o tempo 10, depois estabiliza. A linha média está abaixo da centralidade específica.
Sinistros Ocorridos em Regime de Capitalização: A centralidade aumenta lentamente até o tempo 10 e depois estabiliza. A linha média está abaixo da centralidade específica.
Para a maioria das métricas, a centralidade específica é maior do que a média, sugerindo que esses elementos são mais centrais no grafo comparados com a média de todos os elementos. Algumas métricas, como “Custo de Aquisição” e “Recuperação de Sinistros”, têm centralidade abaixo da média, indicando menor importância relativa no grafo. As flutuações na centralidade específica em relação à média indicam mudanças dinâmicas na importância relativa das diferentes métricas ao longo do tempo.
Centralidade de Proximidade Temporal
O objetivo principal desta centralidade é analisar o quão central um nó é em termos de quando ele se comunica com outros nós ao longo do tempo em um grafo temporal.
Vejamos a seguir os valores de centralidade de proximidade temporal de cada uma das variáveis dos grafos estimados pelo MGM variante no tempo representados na visualização a seguir.
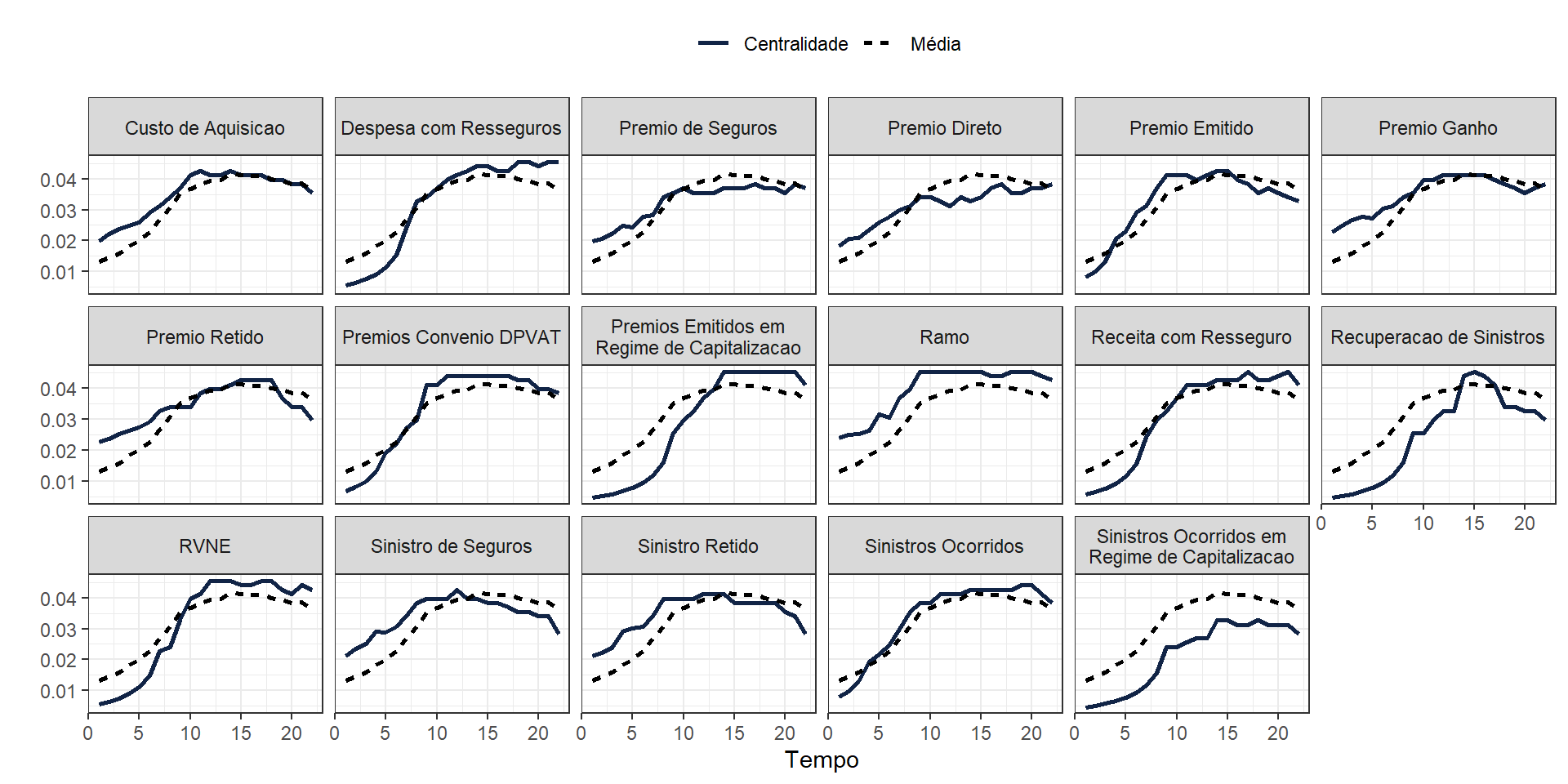
A linha azul sólida representa a centralidade temporal específica para cada variável, enquanto a linha preta tracejada representa a média de todas as centralidades ao longo do tempo. Vamos analisar cada subgráfico individualmente.
Custo de Aquisição: Possui valores decrescentes ao longo do tempo, com a linha se aproximando da média no final do período.
Despesa com Resseguro: Apresenta uma tendência decrescente no início do período, seguida por um aumento até se estabilizar em torno da média no final.
Prêmio de Seguros: Demonstra uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
Prêmio Direto: Apresenta uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
Prêmio Emitido: Demonstra um crescimento constante ao longo do tempo, superando a média em meados do período e se estabilizando acima dela no final.
Prêmio Ganho: Apresenta uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
Prêmio Retido: Possui valores decrescentes ao longo do tempo, se aproximando da média no final do período.
Prêmios Convênio DPVAT: Demonstra um crescimento constante ao longo do tempo, superando a média em meados do período e se estabilizando acima dela no final.
Prêmios Emitidos em Regime de Capitalização: Apresenta uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
Ramo: Possui valores decrescentes ao longo do tempo, se aproximando da média no final do período.
Receita com Resseguro: Apresenta uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
Recuperação de Sinistros: Demonstra um crescimento constante ao longo do tempo, superando a média em meados do período e se estabilizando acima dela no final.
RVNE: Possui valores decrescentes ao longo do tempo, se aproximando da média no final do período.
Sinistro de Seguros: Apresenta uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
Sinistro Retido:Possui valores decrescentes ao longo do tempo, se aproximando da média no final do período.
Sinistros Ocorridos: Demonstra um crescimento constante ao longo do tempo, superando a média em meados do período e se estabilizando acima dela no final.
Sinistros Ocorridos em Regime de Capitalização: Apresenta uma tendência decrescente no início, seguida por um aumento gradual até se estabilizar acima da média no final.
As variáveis relacionadas a custos (aquisição, despesas com resseguros, prêmios retidos e RVNE) apresentam uma tendência decrescente ao longo do tempo, indicando uma maior eficiência na gestão da empresa.
As variáveis relacionadas à receita (prêmios emitido, direto, ganho, convênio DPVAT, receita com resseguros e recuperação de sinistros) apresentam um crescimento constante ou se estabilizam acima da média, demonstrando um aumento na lucratividade da empresa.
As variáveis relacionadas à sinistralidade (sinistros de seguros, retidos e ocorridos) apresentam uma tendência decrescente no início, seguida por um aumento gradual até se estabilizarem acima da média, indicando uma gestão de riscos mais eficaz.
Centralidade de Mediação Temporal
O objetivo principal desta centralidade é analisar o quão os nós se desempenham na comunicação entre outros nós ao longo do tempo em um grafo temporal.
Vejamos a seguir os valores de centralidade de mediação temporal de cada uma das variáveis dos grafos estimados pelo MGM variante no tempo representados na visualização a seguir.
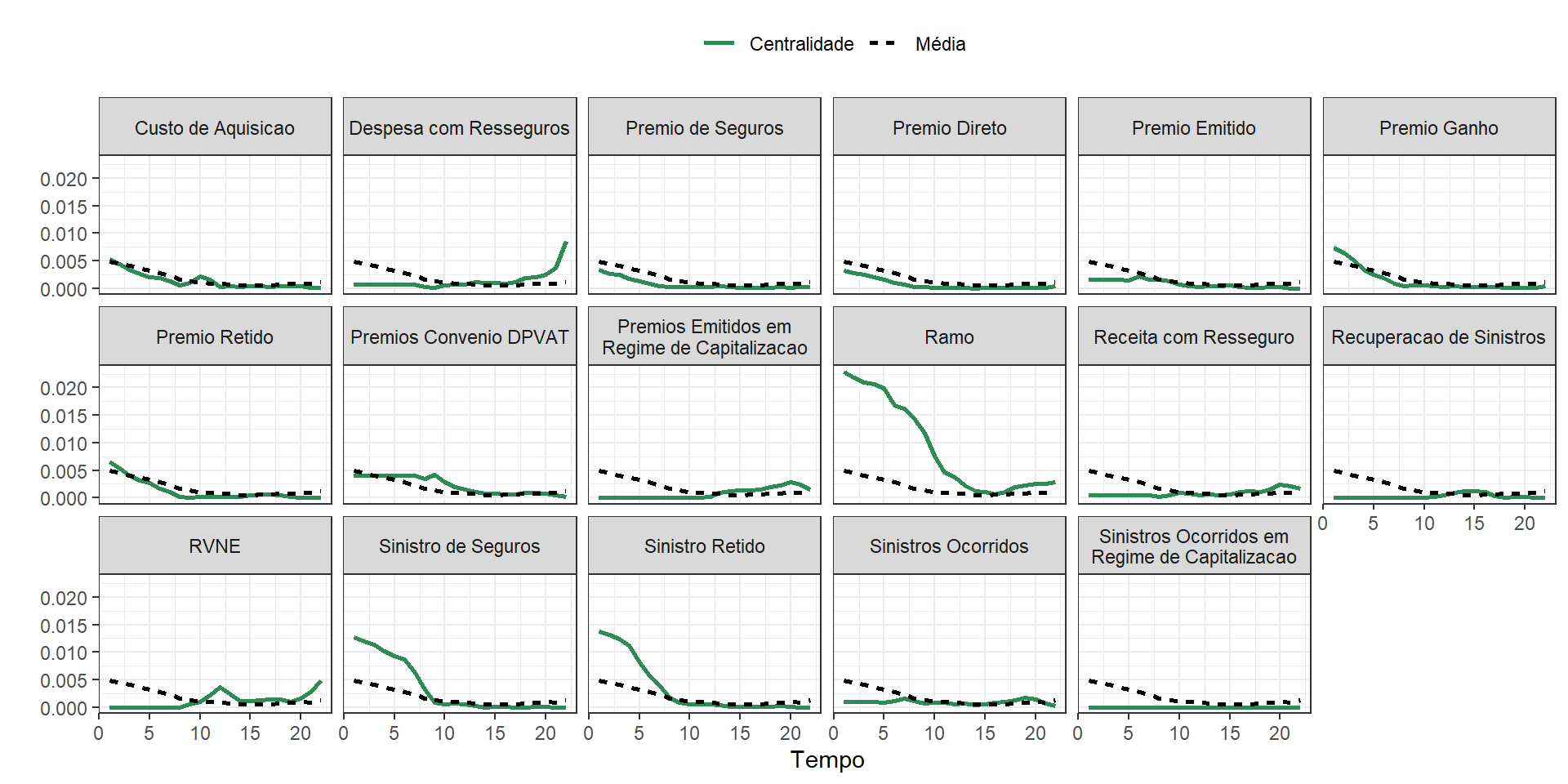
Vejamos quais variáveis mais se distanciaram da média. A linha verde sólida representa a centralidade temporal específica para cada variável, enquanto a linha preta tracejada representa a média de todas as centralidades ao longo do tempo. Vamos analisar alguns subgráfico individualmente.
Ramo: Inicialmente o ramo era um variável totalmente influente na comunição entre as demais, ou seja, para uma variável chegar a outra tinha de “se passar” pelo ramo. Ao longo do tempo essa influênca decresce e se aproxima da média.
Sinistro de Seguros: similarmente ao ramo ocorre para sinistro de seguros, com menor influência. Após o instante de tempo 10 sua centralidade de grau de mediação cai e se aproxima muito da média, que é baixa.
Para a maioria das métricas, a centralidade específica é próximo da média, sugerindo que a medida que o tempo foi passando a necessidade de mediação entre as variáveis foi diminuindo. Algumas métricas, como “Ramo” e “Sinistro de Seguros”, que foram cituadas, têm centralidade inicial acima da média, indicando maior importância de mediação no início da dinâmica dos grafos.
Conclusão
Nesta monografia, exploramos a aplicação de Modelos Gráficos Mistos Variantes no Tempo (MGM) no contexto dos seguros, especificamente utilizando a base de dados de Prêmios e Sinistros do sistema de estatísticas da SUSEP. O MGM provou ser uma ferramenta valiosa para entender como diferentes tipos de variáveis interagem entre si e como essas interações mudam ao longo do tempo.
Através da aplicação do MGM aos dados de Prêmios e Sinistros, conseguimos obter insights valiosos que podem informar decisões estratégicas e políticas no setor de seguros. Em particular, observamos a evolução temporal das características estruturais de centralidade neste modelo gráfico.
As centralidades temporais, que levam em consideração a dimensão temporal, permitiram-nos analisar como as características estruturais de um vértice mudam ao longo do tempo. Isso nos proporcionou uma compreensão mais profunda da estrutura e da dinâmica da rede.
Descobrimos que, para a maioria das métricas, a centralidade específica é maior do que a média, sugerindo que esses elementos são mais centrais no grafo comparados com a média de todos os elementos. No entanto, algumas métricas, como “Custo de Aquisição” e “Recuperação de Sinistros”, têm centralidade abaixo da média, indicando menor importância relativa no grafo.
Além disso, observamos que a necessidade de mediação entre as variáveis foi diminuindo à medida que o tempo passava. Algumas métricas, como “Ramo” e “Sinistro de Seguros”, que foram citadas, têm centralidade inicial acima da média, indicando maior importância de mediação no início da dinâmica dos grafos.
Em resumo, a aplicação do MGM aos dados de Prêmios e Sinistros forneceu uma visão valiosa sobre as tendências e padrões no mercado de seguros brasileiro. No entanto, é importante notar que nosso estudo tem suas limitações e sugere a necessidade de pesquisas futuras para explorar ainda mais o potencial do MGM e das centralidades temporais na análise de dados complexos.
Esperamos que nosso trabalho contribua para a evolução da ciência de dados e das técnicas estatísticas, permitindo o desenvolvimento de modelos cada vez mais sofisticados para a análise de dados complexos. Além disso, esperamos que nossos achados possam informar decisões estratégicas e políticas no setor de seguros, contribuindo para a melhoria e a eficiência do mercado de seguros brasileiro.
Referências
Agresti, A. (2003). Categorical Data Analysis (Vol. 482). John Wiley & Sons.
Chen, S., Witten, D. M., & Shojaie, A. (2015). Selection and Estimation for Mixed Graphical Models. Biometrika, 102(1), 47–64. https://doi.org/10.1093/biomet/asu051
Chen, X., & He, Y. (2018). Inference of High-Dimensional Linear Models with Time-Varying Coefficients. Statistica Sinica, 28(1), 255–276. https://doi.org/10.5705/ss.202015.0202
Freeman, L. C. (1978). Centrality in Social Networks Conceptual Clarification. Social Networks, 1(3), 215–239.
Foygel, R., & Drton, M. (2015). High-Dimensional Ising Model Selection with Bayesian Information Criteria. Electronic Journal of Statistics, 9(1), 567–607. https://doi.org/10.1214/15-ej
Friedman, J., Hastie, T., & Tibshirani, R. (2010). Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software, 33(1), 1–22. https://doi.org/10.18637/jss.v033.i01
Gibberd, A. J., & Nelson, J. D. B. (2017). Regularized Estimation of Piecewise Constant Gaussian Graphical Models: The Group-Fused Graphical Lasso. Journal of Computational and Graphical Statistics, 26(3), 623–634. https://doi.org/10.1080/10618600.2017.1302340
Superintendência de Seguros Privados. Glossário. https://www.gov.br/susep/pt-br/central-de-conteudos/glossario. Acesso em 14/05/2024.
Haslbeck, J. M. B., & Waldorp, L. J. (2020). mgm: Estimating Time-Varying Mixed Graphical Models in High-Dimensional Data. Journal of Statistical Software, 93(8), 1–46. https://doi.org/10.18637/jss.v093.i08
Hastie, T., Tibshirani, R., & Wainwright, M. (2015). Statistical Learning with Sparsity. CRC Press.
Kim, H., & Anderson, R. (2012). Temporal Node Centrality in Complex Networks. Physical Review E, 85(2).
Koller, D., & Friedman, N. (2009). Probabilistic Graphical Models: Principles and Techniques. MIT Press.
Lauritzen, S. L. (1996). Graphical Models. Clarendon Press, Oxford. (Oxford Statistical Science Series, No. 17).
Meinshausen, N., & Bühlmann, P. (2006). High-Dimensional Graphs and Variable Selection with the Lasso. The Annals of Statistics, 34(3), 1436–1462. https://doi.org/10.1214/009053606000000281
Nelder, J. A., & Baker, R. J. (1972). Generalized Linear Models. In Encyclopedia of Statistical Sciences. https://doi.org/10.1002/0471667196.ess0866
R Core Team. (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Schwarz, G. (1978). Estimating the Dimension of a Model. The Annals of Statistics, 6(2), 461–464. https://doi.org/10.1214/aos/1176344136
Superintendência de Seguros Privados. Prêmios e Sinistros. https://www2.susep.gov.br/menuestatistica/SES/premiosesinistros.aspx?id=54. Acesso em 14/05/2024.
Superintendência de Seguros Privados. (2024). Setor de seguros cresce no primeiro trimestre de 2024. https://www.gov.br/susep/pt-br/central-de-conteudos/noticias/2024/maio/setor-de-seguros-cresce-13-7-e-ultrapassa-r-100-bilhoes-em-arrecadacao-no-primeiro-trimestre-de-2024. Acesso em 14/05/2024.
Loh, P. L., & Wainwright, M. J. (2012). Structure Estimation for Discrete Graphical Models: Generalized Covariance Matrices and Their Inverses. In Advances in Neural Information Processing Systems (pp. 2087–2095).
Wainwright, M. J., & Jordan, M. I. (2008). Graphical Models, Exponential Families, and Variational Inference. Foundations and Trends in Machine Learning, 1(1–2), 1–305. https://doi.org/10.1561/2200000001
Yang, E., Baker, Y., Ravikumar, P., Allen, G., & Liu, Z. (2014). Mixed Graphical Models via Exponential Families. In Artificial Intelligence and Statistics (pp. 1042–1050).
Zhou, S., Lafferty, J., & Wasserman, L. (2010). Time-Varying Undirected Graphs. Machine Learning, 80(2–3), 295–319. https://doi.org/10.1007/s10994-010-5180-0